El software DERIVE 5



El software DERIVE 5

¿Qué es DERIVE 5?

     Derive es una aplicación destinada a cualquier estudiante, profesor o profesional que tenga que realizar algún tipo de tarea relacionada con las matemáticas.

    Es uno de los programas más utilizados en entornos relacionados con las matemáticas, universidades y trabajos de ingeniería, ya que es una herramienta de Cálculo Simbólico CAS (Sistema Algebráico Computacional) poderosa y fácil de usar, con máximo poder computacional y capacidad de generar gráficas en tercera dimensión (3-D).

¿Para qué sirve? 

     El software es ampliamente usado para el análisis de problemas matemáticos ya que ofrece una interfaz de fácil uso y se obtienen datos fiables en la resolución de dichos problemas. 

     Integra y resuelve cálculos de algebra, trigonometría, cálculo y algebra lineal eficientemente.

Importancia

     El software Derive 5 es usado en la enseñanza ya que hace más fácil el poder analizar y documentar diferentes aproximaciones en la resolución de problemas.  

     Reduce significativamente el tiempo de cálculo de operaciones laboriosas, lo que permite al usuario reconocer y centrarse en los conceptos importantes del problema resuelto en el software Derive 5. Puede solucionar cálculos simbólicos, problemas numéricos y presentar los resultados como gráficos en segunda y tercera dimensión (2D y 3D ).

Características principales del software

-Gráficos 2D: explícitos, implícitos y paramétricos; coordenadas rectangulares y polares; funciones de variable compleja; especificación de colores; etiquetaje de ejes y anotaciones sobre los gráficos...

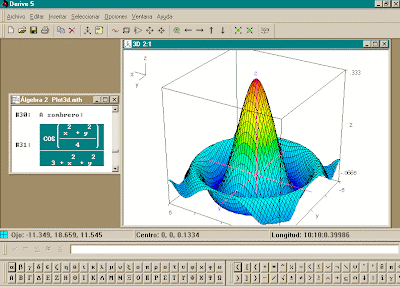
-Gráficos 3D: mallado para funciones de dos variables; selección del punto de vista; cambio de escala; rotación de gráficos en tiempo real...

-Álgebra: desarrollo y factorización de polinomios; simplificación de expresiones algebraicas; resolución de numérica y simbólica; resolución de sistemas lineales de ecuaciones...

-Aritmética: aritmética exacta y aritmética aproximada de precisión configurable; factorización de enteros; conversión de unidades métricas e inglesas; constantes físicas fundamentales...

-Cálculo: cálculo simbólico de límites finitos e infinitos; primera y n-ésima derivadas parciales; integrales definidas e indefinidas; integración numérica; sumas y productos finitos e infinitos; derivación implícita y paramétrica; desarrollos de Taylor y series de Fourier; longitud de arco, áreas y volúmenes; transformadas de Laplace; resolución exacta de EDOs de primer y segundo orden; resolución numérica por Runge-Kutta de sistemas de EDOs...

-Funciones: exponencial, trigonométricas, hiperbólicas, definidas a trozos...

-Programación: definición de funciones; construcciones de control If-then-else; operadores relacionales y booleanos; funciones recursivas e iterativas...

-Vectores, matrices y conjuntos: elementos numéricos y simbólicos; notación estándar de subíndice; producto escalar, matricial y externo; traspuesta, determinante, inversa y traza; valores y vectores propios; algebra no conmutativa; cálculo vectorial diferencial e integral; álgebra tensorial...